Rule of 72

As you save for retirement, there is a simple rule of thumb for determining what your investments will be worth in the future. It is called the “Rule of 72.”

This simple rule quickly tells you how long it takes to double your money at a given rate of return (or interest rate).

Divide 72 by expected rate of return = time to double in value

The result is the time required to double your money—the approximate number of years it will take for your investments to double in value.

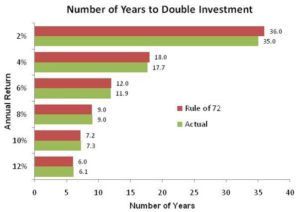
As an example, suppose you expect your investments to average 8% per year. Dividing 72 by 8 equals 9. Hence, it will take about 9 years to double your money if you earn an 8% annual return (excluding taxes and any additional contributions).

Alternatively, if you only expect a 6% return, the rule implies it will take 12 years (72 divided by 6 equals 12) to double your investment.

This simple rule of thumb is remarkably accurate. The result using the Rule of 72 is accurate to within a few months for most rates of return expected from a diversified investment portfolio.

Using the Rule in Retirement Planning

The Rule of 72 is useful in retirement planning to help determine how your retirement savings might grow in the coming years.

For example, say you are 45 years old and plan to retire in 18 year at age 63.

If you currently have $200,000 in retirement investments and expect an 8% investment return, your retirement nest-egg should grow to $800,000 at retirement (doubling twice over 18 years).

As we noted above, at an 8% return, an investment doubles in 9 years. By age 54, the account should have doubled to $400,000, and after another 9 years (at age 63), it will have doubled again to $800,000.

This quick analysis provides a good foundation when deciding how much to save for retirement going forward.

Taking the analysis further, you may instead want to know how your retirement savings will grow on an inflation-adjusted basis. With the Rule of 72, this is a quick adjustment.

Using the same example, assume you expect the same 8% annual return and expect 2% inflation. To determine your real growth, just subtract the 2% inflation rate from the nominal 8% return to get a 6% real annual return. Dividing 72 by 6, we find it will take about 12 years to double your investment in real, inflation-adjusted dollars.

Hence by age 57 you will have the equivalent of $400,000 in today’s dollars. If you wanted $800,000 in inflation-adjusted wealth before you retired, it would take you another 12 years to double again, delaying your retirement to age 69 (assuming you didn’t make additional contributions).

Comparing Investment Options

Thinking about the number of years it takes to double your investment is also an interesting way to compare different investment options.

It has the advantage of considering the power of compounding returns. Return after multiple years as opposed to just the difference during a single year.

Suppose you will buy either 1) a 5-year Certificate of Deposit (CD) with a 2% annually interest rate, or 2) invest in a conservative, diversified portfolio expected to return 6% annually. Although the CD is a safer investment, it also takes nearly 3 times as long to double your money as an investment portfolio returning 6% annually.

By taking the higher investment risk, you are rewarded with a higher expected—but not guaranteed—return on your investments.

Taking this example to an extreme. If you are 30 years old, and plan to retire at age 66, your a CD investment doubles over the next 36 years. Assumes you buy a new CD every 5 years and interest rates stay at 2%.

Alternatively, with the diversified portfolio returning 6% over the next 36 years, you will have 8x your initial investment at retirement. Your money doubles every 12 years.

The net result is a nest-egg 4x larger at retirement. Achieved by selecting the higher return portfolio when you are young.

Of course, this higher return is not guaranteed. The higher return investment will certainly experience a greater level of volatility than a bank CD.